El método de Montecarlo es una potente técnica estadística que utiliza el azar para resolver problemas complejos. Llamado así por el famoso Casino de Montecarlo en Mónaco -conocidopor su asociación con los juegos de azar-, este método se ha convertido en una valiosa herramienta en muchos campos, como la física, las finanzas, la ingeniería y, por supuesto, los juegos de azar.
En esencia, el método de Montecarlo consiste en ejecutar repetidamente simulaciones con entradas aleatorias para aproximar soluciones a problemas que, de otro modo, serían difíciles de calcular. Esto lo hace especialmente adecuado para escenarios en los que el resultado es incierto o en los que muchas variables interactúan de forma impredecible.
El método de Montecarlo permite a jugadores y analistas modelizar juegos, estimar probabilidades y desarrollar estrategias de apuesta en los juegos de azar. Ayuda a responder preguntas como: "¿Cuál es la probabilidad de ganar con esta mano en el póquer?" o "¿Cómo podría funcionar una estrategia de apuestas a lo largo de miles de giros de la ruleta?". Mediante el uso de simulaciones para imitar escenarios de juego de la vida real, el método Monte Carlo proporciona una forma de abordar las incertidumbres inherentes a los juegos de azar.
Comprender el método Monte Carlo
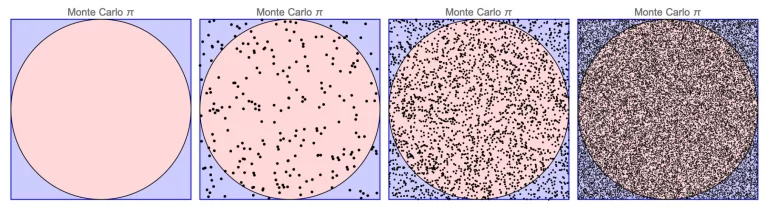
La simulación de Montecarlo es una técnica computacional que utiliza el muestreo aleatorio repetido para obtener resultados numéricos.
La idea central es utilizar el azar para resolver problemas que, en principio, podrían ser deterministas, pero que son demasiado complejos para resolverlos directamente. Mediante la simulación de muchos escenarios, el método de Montecarlo puede proporcionar estimaciones para una amplia gama de problemas, desde el comportamiento de las partículas subatómicas hasta la predicción de los precios de las acciones.
El principio básico del método es sencillo: consiste en crear un modelo del problema, generar entradas aleatorias, ejecutar simulaciones y analizar los resultados. Cuantas más simulaciones se realicen, más precisa será la aproximación, ya que la ley de los grandes números garantiza que la media de los resultados convergerá hacia el valor real.
Por ejemplo, si quieres calcular la probabilidad de ganar una mano de póquer, puedes crear un modelo del juego, repartir miles o incluso millones de manos aleatorias y calcular el porcentaje de veces que esa mano resulta ganadora. Esto aproxima la probabilidad de la mano, aunque el cálculo exacto sea demasiado complejo para derivarlo analíticamente.
El método de Montecarlo es muy valioso cuando se trata de problemas que implican muchas variables o interacciones, en los que los enfoques analíticos tradicionales tienen dificultades. En lugar de resolver estos problemas con una fórmula directa, las simulaciones de Montecarlo descomponen la complejidad en simulaciones manejables, lo que permite explorar distintos resultados y escenarios.
Esta capacidad de modelar y simular sistemas complejos convierte al método de Montecarlo en una herramienta versátil para los juegos de azar, en los que el azar y la probabilidad desempeñan un papel fundamental. Tanto si se trata de estimar los resultados a largo plazo de una estrategia de apuestas como de calcular el valor esperado de un juego, el método de Montecarlo ofrece una forma práctica de sortear la incertidumbre y tomar decisiones con mayor conocimiento de causa.
Historia de la simulación de Montecarlo
El método de Montecarlo tiene sus raíces a principios del siglo XX y ha evolucionado considerablemente. Su nombre procede del famoso Casino de Montecarlo, en Mónaco, y refleja el elemento de aleatoriedad y azar intrínseco al juego y a las simulaciones estadísticas.
Los orígenes del método de Montecarlo se remontan al desarrollo de la teoría de la probabilidad en el siglo XVII. Matemáticos como Blaise Pascal y Pierre de Fermat sentaron las bases para comprender los sucesos aleatorios, que más tarde servirían de base a los principios estadísticos que sustentan la técnica de Montecarlo. Sin embargo, no fue hasta el siglo XX cuando estos conceptos teóricos empezaron a aplicarse en contextos prácticos y computacionales.
El método tal y como lo conocemos hoy surgió durante la Segunda Guerra Mundial, principalmente gracias al trabajo de científicos y matemáticos que participaron en el Proyecto Manhattan. Los físicos Stanislaw Ulam y John von Neumann desempeñaron un papel crucial en su desarrollo. Ulam empezó a explorar la idea de utilizar el muestreo aleatorio para resolver problemas matemáticos complejos, sobre todo de física nuclear y radiación, mientras se recuperaba de una enfermedad.
El concepto se formalizó cuando Ulam y von Neumann desarrollaron una técnica para modelizar el comportamiento de las partículas en diversos escenarios, utilizando números aleatorios para simular los resultados. Este trabajo sentó las bases de lo que se convertiría en el método de Montecarlo.
Ulam y von Neumann acuñaron el nombre de "Montecarlo" debido a la dependencia inherente del método en la aleatoriedad, paralela a la imprevisibilidad de los resultados de las apuestas. La asociación con el Casino de Montecarlo ponía de relieve la naturaleza lúdica e incierta de las simulaciones que creaban.
Aunque el método se desarrolló inicialmente para aplicaciones científicas y de ingeniería, sus principios han sido adoptados por la comunidad del juego. Los jugadores empezaron a aplicar las simulaciones de Montecarlo para analizar estrategias de juego, evaluar probabilidades y comprender las probabilidades de distintos resultados. Modelando miles de manos de póquer o giros de la ruleta, los jugadores pueden obtener información para tomar sus decisiones de apuesta.
Hoy en día, el método de Montecarlo se utiliza ampliamente en diversas disciplinas, desde las finanzas y la ingeniería hasta la informática y la inteligencia artificial. En los juegos de azar, sigue siendo una herramienta valiosa para los jugadores profesionales y los aficionados ocasionales, ya que proporciona información sobre la estrategia y la gestión del riesgo.
Simulación de Montecarlo en los juegos de azar
El método de Montecarlo ha encontrado un encaje natural en los juegos de azar, donde la aleatoriedad y la probabilidad son el nombre del juego. Mediante la simulación de varios resultados de juegos de azar, permite a los jugadores y analistas obtener información sobre probabilidades, rendimientos esperados y riesgos potenciales, proporcionando una comprensión más profunda de cómo las diferentes estrategias podrían funcionar a lo largo del tiempo.
La esencia del método de Montecarlo en los juegos de azar consiste en utilizar simulaciones repetidas para estimar las probabilidades y los resultados de distintos juegos.
Por ejemplo, en lugar de basarse únicamente en cálculos teóricos de probabilidades, los jugadores pueden ejecutar miles o incluso millones de rondas de juego simuladas para observar los resultados probables. Este enfoque ayuda a modelar las condiciones del mundo real con mayor precisión, incluidas las variaciones y rachas que son difíciles de tener en cuenta en la probabilidad básica.
Las simulaciones de Monte Carlo pueden aplicarse a casi cualquier escenario de juego. Tanto si se trata de hacer girar una ruleta, como de repartir una mano de póquer o jugar a una máquina tragaperras, el método permite a los jugadores simular y analizar los posibles resultados, proporcionando estimaciones de las tasas de ganancias, los pagos y la rentabilidad a largo plazo de determinadas apuestas.
Simulación de Monte Carlo para la ruleta
Veamos cómo puede aplicarse el método de Monte Carlo a un juego sencillo como la ruleta. En la ruleta europea, hay 37 números: 1-36 y un único cero. La tarea podría consistir en estimar la probabilidad de que un número salga en rojo. Mediante una simulación Monte Carlo, se podrían simular, por ejemplo, 100.000 giros de una ruleta virtual. En cada giro se genera un número aleatorio, y si corresponde a un número rojo, se cuenta como ganancia. Una vez completadas todas las tiradas, la proporción de victorias calcula la probabilidad de caer en rojo.
Mediante este proceso, la simulación de Monte Carlo mostraría que la probabilidad de obtener un número rojo en la ruleta europea es de aproximadamente el 48,65%, lo que se aproxima mucho a la probabilidad teórica real. Este método es especialmente útil cuando se trata de comprender el rendimiento de determinadas estrategias de apuesta a lo largo de muchas tiradas, ya que ayuda a evaluar los riesgos y las posibles recompensas.
| Nombre | Los productores | volver al jugador | |||
|
|
98.65% | Play | |||
|
|
98.65% | Play | |||
|
|
98.65% | Play | |||
|
|
98.65% | Play | |||
|
|
98.65% | Play | |||
|
|
98.6% | Play | |||
|
|
97.3% | Play | |||
|
|
97.3% | Play | |||
|
|
97.3% | Play | |||
|
|
97.3% | Play |
Simulación Monte Carlo para Póquer
Manos En el póquer, los jugadores a menudo necesitan calcular la probabilidad de ganar con una mano específica contra oponentes potenciales. En este caso, se puede utilizar una simulación Monte Carlo para estimar la probabilidad de diferentes resultados. Por ejemplo, en Texas Hold'em, puede que quiera saber la probabilidad de ganar con una pareja de ases contra una serie de manos posibles.
Realizando una simulación Monte Carlo, puede simular miles de manos repartidas con varias cartas y calcular con qué frecuencia la pareja de ases saldría ganadora. La simulación puede proporcionar una probabilidad de ganar basada en todos los escenarios posibles, ayudando al jugador a tomar mejores decisiones sobre cuándo apostar, subir o retirarse.
Estos ejemplos ilustran cómo el método de Monte Carlo permite a los jugadores ir más allá de la intuición o la estrategia básica, utilizando datos para informar su juego.
Aplicaciones para jugadores con ventaja
El método Monte Carlo no es sólo una herramienta para los jugadores ocasionales; también es valioso para los jugadores con ventaja, aquellos que utilizan diversas técnicas para inclinar las probabilidades a su favor. Estos jugadores se basan en un profundo conocimiento de la probabilidad, la estrategia y el riesgo, y el método Monte Carlo ofrece una manera de perfeccionar sus enfoques a través de simulaciones detalladas.
He aquí algunas aplicaciones clave del método Monte Carlo para los jugadores de ventaja.
Contar cartas en el Blackjack
Una de las técnicas de juego con ventaja más conocidas es el conteo de cartas en el blackjack. Haciendo un seguimiento de las cartas que se han repartido, los contadores de cartas pueden estimar la probabilidad de que aparezcan ciertas cartas en las próximas manos, ajustando así sus apuestas y su estrategia de juego en consecuencia. El método Monte Carlo puede ayudar en este proceso simulando miles de partidas de blackjack en diferentes condiciones.
Por ejemplo, un jugador podría utilizar simulaciones Monte Carlo para ver cómo afecta el conteo de cartas a la probabilidad de ganar en varios momentos de la partida. Podrían simular escenarios con diferentes conteos y estrategias de apuesta para encontrar el enfoque óptimo. Las simulaciones pueden ayudar a responder preguntas como: "¿Cuál es el beneficio esperado si doblo mi apuesta cuando el recuento es +2?". Al ejecutar estas simulaciones, los contadores de cartas pueden afinar su enfoque para maximizar los beneficios y minimizar los riesgos.
| Nombre | Los productores | volver al jugador | ||
|
|
99.78% | |||
|
|
99.71% | |||
|
|
99.7% | |||
|
|
99.69% | |||
|
|
99.65% | |||
|
|
99.6% | |||
|
|
99.59% | |||
|
|
99.54% | |||
|
|
99.54% | |||
|
|
99.54% |
Estrategias de apuestas y gestión de fondos
Las simulaciones Monte Carlo también son herramientas valiosas para probar diferentes estrategias de apuestas. Las estrategias más comunes, como el sistema Martingala o el Criterio de Kelly, se basan en ajustar el tamaño de las apuestas en función de las ganancias y las pérdidas. Pero antes de utilizar estas estrategias en juegos reales, los jugadores a menudo quieren entender sus efectos a largo plazo, especialmente en lo que respecta a la gestión del bankroll.
Con el método Monte Carlo, los jugadores pueden simular miles de sesiones de apuestas, aplicando cada vez una estrategia concreta. Esto les permite ver el impacto en su bankroll a lo largo del tiempo, incluidas las rachas de victorias y derrotas. Por ejemplo, si los jugadores quieren comprobar cómo se comporta la estrategia Martingale en un juego como la ruleta, pueden simular una serie de apuestas con resultados variables. Esto ayuda a revelar el potencial de oscilaciones considerables en el bankroll y el riesgo de quedarse sin dinero durante una racha perdedora.
Los jugadores pueden comprender mejor el equilibrio entre riesgo y recompensa simulando distintas estrategias de apuesta y tomando decisiones informadas sobre cuánto apostar, cuándo parar y qué estrategias evitar. Por ejemplo, podrían descubrir que la estrategia Martingala, aunque tentadora, conlleva un riesgo significativo de agotar rápidamente sus fondos si se produce una racha perdedora, mientras que el Criterio de Kelly podría proporcionar un enfoque más equilibrado para gestionar el riesgo.
Simulación de los resultados del juego para una estrategia óptima
Los jugadores con ventaja a menudo se centran en encontrar la estrategia óptima para un determinado juego o escenario, y el método Monte Carlo puede ser decisivo en esta búsqueda. Por ejemplo, en el video póquer, los jugadores tienen que decidir qué cartas conservar y cuáles descartar en función del valor esperado de cada decisión. Una simulación de Montecarlo puede ayudar simulando todos los resultados posibles para diferentes elecciones y comparando sus valores esperados.
De este modo, los jugadores pueden determinar qué jugadas maximizan sus posibilidades de ganar a lo largo del tiempo. El método puede utilizarse para calcular la expectativa a largo plazo de cada decisión posible, proporcionando una base respaldada por datos para tomar decisiones óptimas. Este enfoque no se limita al póquer, sino que también puede aplicarse a otros juegos de habilidad como el blackjack, el bacará o incluso a escenarios específicos de apuestas deportivas.
Estas aplicaciones demuestran cómo el método Monte Carlo permite a los jugadores aventajados profundizar en la dinámica del juego, probar teorías y encontrar ventajas que los jugadores ocasionales podrían pasar por alto.
Herramientas y software para simulaciones Monte Carlo
Si bien el método Monte Carlo puede realizarse manualmente con tiempo y paciencia suficientes, el uso de herramientas y software especializados puede agilizar el proceso de forma significativa, facilitando la ejecución de simulaciones a gran escala de forma rápida y precisa. Muchas de estas herramientas son accesibles tanto para principiantes como para usuarios avanzados, lo que permite a los apostantes analizar escenarios complejos con facilidad.
A continuación se ofrece una visión general de las herramientas y el software más populares para ejecutar simulaciones Monte Carlo en los juegos de azar.
- Excel con VBA (Visual Basic for Applications) es una herramienta muy utilizada para crear simulaciones Monte Carlo sencillas, especialmente cuando se combina con VBA. VBA permite a los usuarios automatizar el proceso de simulación escribiendo pequeños programas para generar números aleatorios y realizar un seguimiento de los resultados. Excel es ideal para simular juegos de azar más sencillos, como lanzar monedas, tirar dados o juegos de cartas básicos. También puede utilizarse para simular estrategias de apuestas automatizando los cálculos de ganancias, pérdidas y ajustes en el bankroll.
- Python es un lenguaje de programación versátil muy popular para el análisis de datos y las simulaciones. Cuenta con bibliotecas como NumPy para la generación de números aleatorios y Pandas para la manipulación de datos, lo que lo convierte en una buena opción para ejecutar simulaciones Monte Carlo. Python puede manejar simulaciones complejas, como el cálculo de probabilidades de manos de póquer, el modelado de estrategias de ruleta o la simulación de miles de giros en máquinas tragaperras. Es especialmente útil cuando se trabaja con grandes conjuntos de datos o cuando hay que simular múltiples escenarios.
- R es un lenguaje de programación estadística que destaca en el análisis y la visualización de datos, lo que lo convierte en una gran opción para las simulaciones Monte Carlo. R es muy adecuado para simular escenarios que requieren un fuerte enfoque en el análisis estadístico, como el análisis de la varianza de diferentes estrategias de apuestas o el cálculo del valor esperado en juegos de cartas complejos.
- @RISK, Simul8 y otros paquetes especializados están diseñados para este tipo de simulaciones. Estas herramientas suelen tener funciones integradas para crear simulaciones, generar variables aleatorias y analizar los resultados. También pueden utilizarse para probar sistemas de apuestas complejos, ejecutar miles de simulaciones de partidas y generar informes detallados.
- Los simuladoresy las calculadoras en línea permiten a los usuarios ejecutar simulaciones de Monte Carlo directamente en su navegador, sin necesidad de descargar ningún software ni escribir código. Los simuladores en línea pueden ser una forma estupenda de analizar rápidamente juegos más sencillos, como tiradas de dados, lanzamientos de monedas o manos de blackjack. Suelen tener configuraciones y modelos predefinidos para juegos de azar populares.
Estas herramientas y software permiten a los jugadores ejecutar simulaciones Monte Carlo de forma eficaz para analizar sus juegos y estrategias.
Pros y contras del método Monte Carlo en el juego
Aunque el método Monte Carlo es una herramienta poderosa para analizar y simular escenarios de juego, tiene sus puntos fuertes y débiles. Entender estos beneficios y limitaciones es crucial para los jugadores que quieren utilizar este método de manera efectiva para mejorar sus estrategias y la toma de decisiones.
Ventajas
- Modela escenarios complejos: Una de las mayores ventajas del método Monte Carlo es su capacidad para modelar sistemas complejos en los que múltiples variables interactúan de forma impredecible. En los juegos de azar, incluso los juegos con reglas intrincadas y múltiples resultados posibles, como el póquer o las apuestas deportivas, pueden simularse para evaluar diferentes probabilidades y resultados.
- Permite probar estrategias: El método Monte Carlo permite a los jugadores probar diversas estrategias de apuesta antes de comprometer dinero real. Por ejemplo, un jugador puede simular el rendimiento de un sistema Martingale o Paroli en miles de partidas, lo que le ayuda a comprender los posibles riesgos y beneficios sin tener que experimentarlos en un casino real.
- Ayuda en la gestión de riesgos: Al simular una amplia gama de escenarios, el método Monte Carlo ofrece a los jugadores una imagen más clara de los posibles riesgos y de cómo estos riesgos pueden afectar a sus fondos. Por ejemplo, los jugadores pueden estimar las posibilidades de entrar en una racha perdedora que podría agotar su bankroll, lo que les permite planificar cantidades de apuestas más seguras.
- Proporciona información sobre el valor esperado: El valor esperado (VE) es un concepto crucial en las apuestas, que representa el resultado medio de una apuesta concreta a lo largo del tiempo. El método Monte Carlo puede ayudar a estimar el VE de diferentes apuestas o manos en juegos como el blackjack o el póquer, orientando a los jugadores sobre si jugar de forma agresiva o conservadora en función de su ventaja calculada.
- Informa la toma de decisiones a largo plazo: Dado que el método Monte Carlo puede simular miles o millones de rondas de juego, ayuda a los jugadores a comprender el rendimiento a largo plazo de sus estrategias. Esto es especialmente útil en juegos con poca ventaja para la casa, donde el comportamiento a largo plazo de las apuestas puede diferir significativamente de los resultados a corto plazo.
Limitaciones
- Intensidad computacional: Ejecutar simulaciones Monte Carlo puede requerir una importante potencia de cálculo, especialmente cuando se simulan juegos complejos con muchas variables. Por ejemplo, simular millones de manos de póquer con diferentes estrategias de jugador puede exigir un tiempo de procesamiento considerable, incluso con ordenadores modernos.
- Aproximaciones, no certezas: Aunque las simulaciones Monte Carlo pueden proporcionar estimaciones y probabilidades, no garantizan los resultados. Los resultados se basan en una muestra de escenarios posibles, lo que significa que pueden estar influidos por la aleatoriedad inherente a cada simulación. En consecuencia, las simulaciones pueden producir a veces resultados que se desvíen de las probabilidades teóricas.
- Dependencia de modelos precisos: La precisión de una simulación Monte Carlo depende en gran medida de la calidad del modelo utilizado. Por ejemplo, si una simulación de póquer no tiene en cuenta adecuadamente cómo juegan o farolean los oponentes, las probabilidades resultantes pueden ser engañosas. Esto significa que los jugadores necesitan tener un buen conocimiento del juego que están modelando para construir simulaciones precisas.
- Utilidad limitada para el análisis a corto plazo: Mientras que el método Monte Carlo sobresale en el análisis de probabilidades a largo plazo, es menos eficaz para la comprensión de las tendencias a corto plazo o rachas, a menudo el foco de muchos jugadores. Por ejemplo, puede que no prediga cuándo terminará una racha perdedora o cuándo se producirá la próxima ganancia en juegos como las tragaperras.
- Requiere conocimientos de probabilidad y estadística: Utilizar eficazmente el método Monte Carlo requiere conocimientos básicos de probabilidad, estadística y programación (si se utilizan herramientas como Python o R). Para algunos jugadores, la curva de aprendizaje puede ser empinada, lo que dificulta el uso de este método sin invertir tiempo en dominar los conceptos subyacentes.
Sopesando estas ventajas y limitaciones, los jugadores pueden decidir cuándo y cómo utilizar el método Monte Carlo para mejorar su comprensión de los juegos.
Ejemplos de simulaciones de Monte Carlo en juegos de casino populares
Para entender las aplicaciones prácticas del método de Montecarlo en el juego, es útil ver ejemplos específicos en juegos de casino populares.
Blackjack: Cálculo del valor esperado de una estrategia
- Escenario: Un jugador quiere saber el valor esperado (VE) de jugar una estrategia específica de blackjack, como pedir siempre con un 17 blando o doblar en ciertas manos. El método Monte Carlo permite al jugador simular miles de rondas de blackjack utilizando esta estrategia para ver cómo se comporta a lo largo del tiempo.
- Configuración de la simulación: El jugador crea una baraja virtual y escribe un programa (o utiliza software) que reparte las cartas según las reglas del blackjack, simula la estrategia elegida y registra el resultado de cada ronda. Repite este proceso durante 100.000 manos o más.
- Resultados: La simulación calcula el porcentaje de manos ganadas, perdidas o empujadas, y el rendimiento general de la inversión (ROI) para la estrategia. Por ejemplo, el jugador puede descubrir que pedir un 17 blando conlleva un menor rendimiento a largo plazo que quedarse parado. Los datos pueden guiar al jugador hacia las opciones más rentables en futuras partidas.
Póquer: Simulación de probabilidades de mano
- Escenario: En el póquer Texas Hold'em, un jugador quiere estimar sus posibilidades de ganar con una pareja de reinas contra otros dos oponentes con manos desconocidas. En lugar de confiar en las tablas de probabilidades de póquer, utilizan el método Monte Carlo para simular miles de partidas con diferentes manos posibles para los oponentes.
- Configuración de la simulación: El jugador crea un programa que genera aleatoriamente las cartas comunitarias y las posibles manos de los oponentes para cada partida simulada. El resultado se registra en cada partida para determinar si la pareja de reinas gana, empata o pierde.
- Resultados: Después de simular 1.000.000 de manos, el jugador puede ver que su pareja de reinas gana aproximadamente el 65% de las veces contra dos oponentes aleatorios. Esta información ayuda al jugador a decidir si igualar, subir o retirarse en situaciones reales de juego, basándose en la probabilidad estimada de ganar.
Ruleta: Probar un sistema de apuestas
- Escenario: Un jugador quiere evaluar el sistema de apuestas Martingale en la ruleta europea, en el que dobla su apuesta después de cada pérdida y se restablece después de una ganancia. Quiere saber el riesgo de quiebra y cómo se comporta la estrategia en sesiones largas.
- Configuración de la simulación: Utilizando el método Monte Carlo, el jugador simula 100.000 sesiones de 200 tiradas cada una, empezando con un bankroll específico y aplicando la estrategia Martingale. Cada sesión termina cuando el jugador alcanza un objetivo de beneficios o se queda sin dinero.
- Resultados: La simulación muestra que, aunque el sistema de Martingala puede lograr pequeñas ganancias con frecuencia, existe un riesgo significativo de llegar a una larga racha perdedora que agote rápidamente el bankroll del jugador. Los resultados revelan que el resultado esperado de la estrategia es negativo a lo largo del tiempo debido a la ventaja de la casa, lo que la hace arriesgada para el juego prolongado. Esto permite al jugador comprender los peligros de utilizar un sistema de este tipo.
Máquinas Tragamonedas: Comprender la Varianza y la Volatilidad
- Escenario: Un jugador de tragaperras está interesado en entender la volatilidad de un juego de tragaperras en particular. Quiere estimar con qué frecuencia es probable que le toque el premio gordo o que experimente largas rachas perdedoras.
- Configuración de la simulación: El jugador utiliza una simulación Monte Carlo para replicar la tabla de pagos de la máquina tragaperras y simular millones de tiradas, con cada tirada determinando aleatoriamente los resultados en función del RTP (Return to Player) de la máquina y la frecuencia de aciertos.
- Resultados: La simulación proporciona un desglose detallado de la frecuencia con la que se producen los distintos pagos, la duración típica de las rachas ganadoras y perdedoras y el tiempo medio que transcurre entre un premio y otro. Esto ayuda al jugador a calibrar si el juego se adapta a sus preferencias de riesgo y recompensa, por ejemplo, si prefiere pequeñas ganancias frecuentes o la posibilidad de obtener pagos mayores.
Estos ejemplos demuestran lo versátil y potente que puede ser el método Monte Carlo para los jugadores.
| Nombre | volver al jugador | Pago máximo | Diferencia | Los productores | ||
| 99.07% | x1000 | Low |
|
Play | ||
| 99% | x12075 | High |
|
Play | ||
| 98.98% | x3843 | Middle |
|
Play | ||
| 98.6% | x670 | Low |
|
Play | ||
| 98.18% | — | Low |
|
Play | ||
| 98.13% | x15000 | High |
|
Play | ||
| 98.12% | x10000 | High |
|
Play | ||
| 98.12% | x500 | Low |
|
Play | ||
| 98.11% | x100 | Middle |
|
Play | ||
| 98.11% | x1500 | High |
|
Play | ||
| 98.08% | x9000 | Low |
|
Play | ||
| 98.08% | x10000 | High |
|
Play | ||
| 98.08% | x10000 | High |
|
Play | ||
| 98.07% | x2500 | High |
|
Play | ||
| 98.07% | x3000 | High |
|
Play |
Consejos para utilizar eficazmente el método Monte Carlo en los juegos de azar
Para maximizar los beneficios del método Monte Carlo, es importante que los jugadores lo apliquen cuidadosamente. He aquí algunos consejos prácticos para utilizar esta técnica con eficacia, garantizando que las simulaciones sean precisas, perspicaces y se ajusten a los escenarios del mundo real.
1. 1. Empezar con objetivos claros
- Defina el problema: Antes de ejecutar cualquier simulación, tenga una idea clara de lo que quiere conseguir. ¿Está probando la rentabilidad a largo plazo de un sistema de apuestas, evaluando la varianza de un juego específico o comprendiendo el riesgo de ruina para un determinado tamaño de bankroll? Un objetivo claro garantiza que la simulación se diseñe correctamente y que se centre en los datos relevantes.
- Identifique las variables clave: Determine qué variables son las más importantes para su simulación, como las probabilidades de ganar, el tamaño de las apuestas, las reglas del juego o la duración de una sesión. Centrarse en estos factores críticos puede hacer que sus simulaciones sean más eficientes y evitar que pierda tiempo modelando detalles innecesarios.
2. 2. Utilice datos realistas
- Recopile datos precisos: La precisión de una simulación Monte Carlo depende de la calidad de los datos que utilice. Si está simulando manos de póquer, utilice distribuciones de cartas y probabilidades realistas. Para las apuestas deportivas, base sus datos en estadísticas de juego reales y datos de rendimiento de los jugadores. Cuanto más realistas sean sus datos, más fiables serán sus resultados.
- Tengaen cuenta la ventaja de la casa: Incluya siempre la ventaja de la casa en sus cálculos cuando simule juegos de casino. Esta es la ventaja incorporada que el casino tiene sobre el jugador. Al incluir la ventaja de la casa, tus simulaciones reflejarán mejor los resultados del mundo real y te ayudarán a entender el impacto de esta ventaja en tu estrategia.
3. Ejecute un número suficiente de simulaciones
- Evite las muestras pequeñas: Ejecutar sólo unas pocas simulaciones puede producir resultados sesgados por el azar. Para obtener una estimación fiable, intente realizar miles o incluso millones de iteraciones, dependiendo de la complejidad del juego y del número de variables. Una muestra de mayor tamaño proporciona una imagen más precisa de los posibles resultados y reduce la influencia de los valores atípicos.
- Compruebe la convergencia: Compruebe si los resultados de la simulación se estabilizan a medida que aumenta el número de iteraciones. Por ejemplo, si está estimando la tasa de ganancias de una mano de póquer, el porcentaje debería estabilizarse en torno a un valor determinado a medida que aumenta el número de manos simuladas. Esto indica que la simulación ha alcanzado un resultado fiable.
4. Interpretar los resultados con precaución
- Comprenda la variabilidad: Incluso con un gran número de simulaciones, los resultados de un método Monte Carlo reflejan la distribución de resultados potenciales más que predicciones exactas. Tenga en cuenta que los resultados a corto plazo en sesiones de juego reales pueden variar significativamente de la media simulada.
- Utilice intervalos de confianza: Cuando analice los resultados de su simulación, considere la posibilidad de utilizar intervalos de confianza para comprender el rango dentro del cual es probable que se sitúen los resultados. Esto puede ayudarle a captar la variabilidad potencial y evitar poner demasiado énfasis en una estimación de un solo punto.
5. 5. Centrarse en el análisis a largo plazo
Simule sesiones prolongadas: Los resultados de las apuestas pueden ser muy variables a corto plazo, por lo que utilizar el método Monte Carlo para simular periodos más largos -como miles de tiradas o manos- proporciona una visión más clara de la viabilidad a largo plazo de una estrategia. Esto es especialmente importante para entender juegos como el blackjack, en el que las pequeñas ventajas se acumulan con el tiempo. Planifique las fluctuaciones del bankroll: Utiliza tus simulaciones para anticiparte a las fluctuaciones de tu bankroll a lo largo del tiempo. Por ejemplo, entender la probabilidad de experimentar una serie de pérdidas le ayuda a establecer límites de bankroll más realistas y evitar quedarse sin fondos antes de tiempo.
6. Combine Monte Carlo con otras técnicas analíticas
- Combínelo con el análisis estadístico: Las simulaciones Monte Carlo son sólo una parte de las herramientas de un jugador. Combinarlas con otros métodos estadísticos, como el análisis de regresión o las pruebas de hipótesis, puede proporcionar una imagen más completa de un juego o estrategia. Por ejemplo, después de ejecutar una simulación, puede analizar los resultados para determinar qué variables influyen más en los resultados.
- Comparar con probabilidades teóricas: Después de ejecutar sus simulaciones, compare los resultados con las probabilidades teóricas conocidas para el juego que está estudiando. Esto ayuda a verificar que su simulación está funcionando correctamente y se alinea con las probabilidades esperadas, sirviendo como una verificación de cordura para su modelo.
7. Tenga en cuenta el tiempo y los recursos informáticos
- Optimice sus simulaciones: Si realiza simulaciones en un ordenador doméstico o con una configuración de software sencilla, considere formas de optimizar su código o modelo para reducir el tiempo de cálculo. Esto podría implicar la simplificación de los cálculos, la reducción del número de variables de seguimiento o el uso de algoritmos más eficientes.
- Utilice la computación en nube para grandes simulaciones: Si necesita ejecutar simulaciones especialmente grandes o complejas, el uso de servicios de computación en nube puede acelerar el proceso. Muchas plataformas en la nube permiten alquilar potencia de cálculo en función de las necesidades, lo que facilita el manejo de los grandes conjuntos de datos necesarios para el análisis detallado de Monte Carlo.
8. Aprenda de la comunidad
- Únase a foros y grupos en línea: Hay muchas comunidades en línea donde los jugadores y entusiastas de los datos comparten sus experiencias con las simulaciones Monte Carlo. Sitios web como GitHub, Stack Overflow y foros dedicados a los juegos de azar suelen tener código de ejemplo, debates y estrategias que pueden ayudarle a perfeccionar sus propias simulaciones.
- Estudie los análisis publicados: Muchos apostantes experimentados publican sus análisis o escriben sobre sus enfoques para utilizar simulaciones Monte Carlo en libros, blogs o artículos. Estudiar estos recursos puede ofrecerle nuevas ideas y métodos que quizá no había considerado, ayudándole a mejorar sus propias simulaciones.
Este enfoque permite una mejor preparación, una comprensión más profunda y una ventaja más estratégica tanto en los juegos de casino como en las apuestas deportivas, aprovechando al máximo esta poderosa herramienta matemática.
Reflexiones finales
El método Monte Carlo ofrece un marco poderoso para los jugadores que buscan mejorar su comprensión del riesgo, la probabilidad y la estrategia en diversos escenarios de juego. Aprovechando esta técnica, los jugadores pueden simular innumerables resultados, evaluar la eficacia de diferentes estrategias y tomar decisiones basadas en datos que podrían conducir a un mejor rendimiento en las mesas o durante las apuestas deportivas.
En conclusión, el método de Montecarlo no es sólo una técnica matemática; es un poderoso aliado para los jugadores que pretenden comprender los entresijos de sus juegos.
Al adoptar este método, los jugadores pueden mejorar su proceso de toma de decisiones, gestionar los riesgos de manera más eficaz y, en última instancia, disfrutar de una experiencia de juego más estratégica e informada. Como ocurre con todas las herramientas, la clave está en comprender su aplicación y aprovecharla sabiamente para navegar por el apasionante e impredecible mundo del juego.

































































